1、简介
分类刷算法题(语言:java):
博主将陆续按分类顺序发布力扣算法题的解析与代码。部分代码参考力扣解析,仅供参考,如有疑问,评论探讨。
数组篇:
遇到不会的排序试试
正向走不通反向思考
2、例题推荐
2.1、数组的遍历
485. 最大连续 1 的个数
题目:

1 | class Solution { |

495.提莫攻击
题目:

1 | class Solution { |
414.第三大的数
题目:
1 | class Solution { |
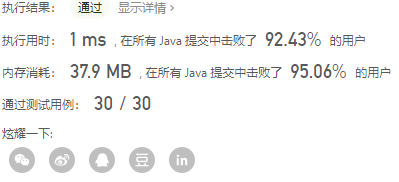
628.三个数的最大乘积
题目:
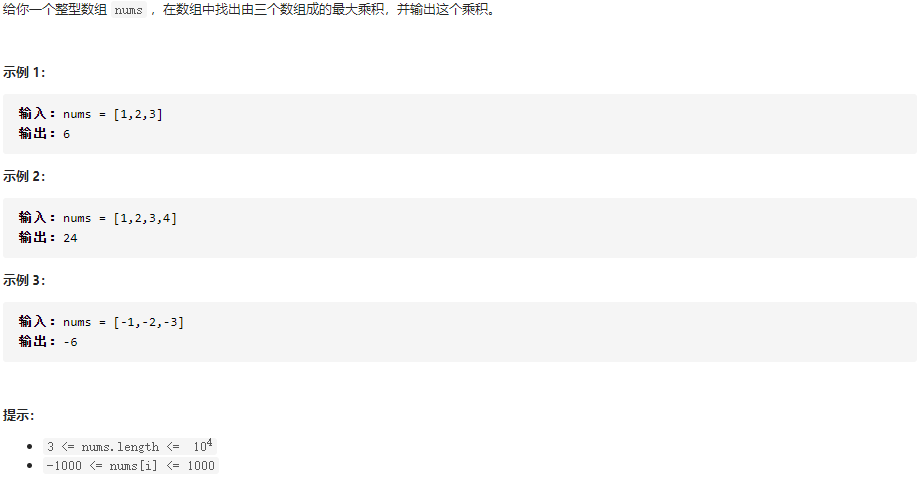
1 | class Solution { |
2.2、统计数组中的元素
645.错误的集合
题目:
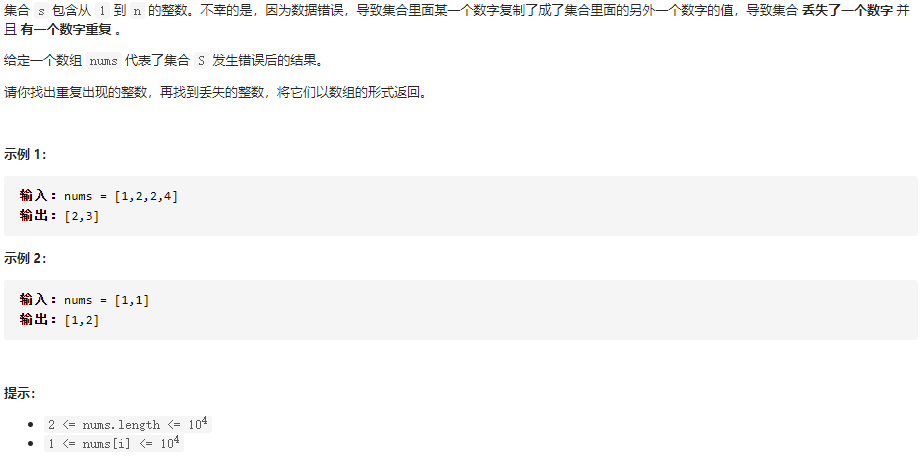
1 | class Solution { |
697.数组的度
题目:
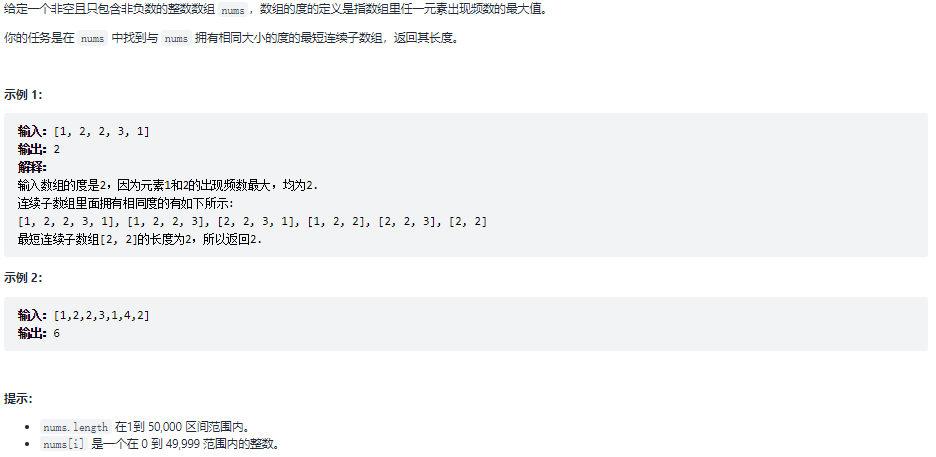
1 | class Solution { |
448.找到所有数组中消失的数字
题目:
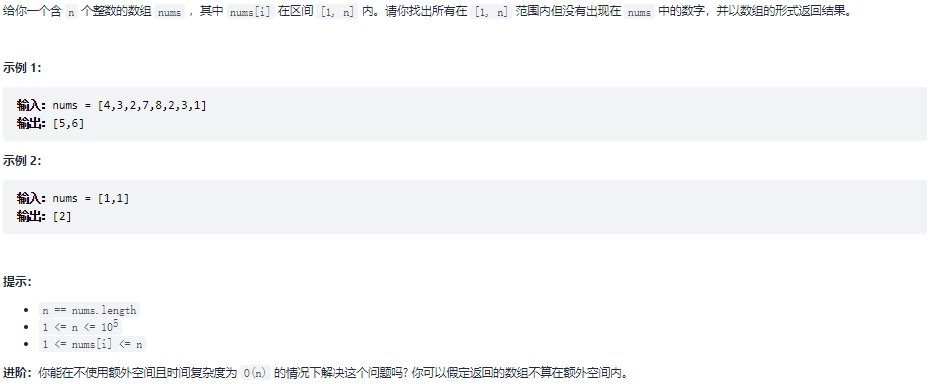
1 | // 数组记录法,需要额外数组记录数值是否出现 |
1 | //哈希记录,在原数组进行记录,不实用额外空间 |
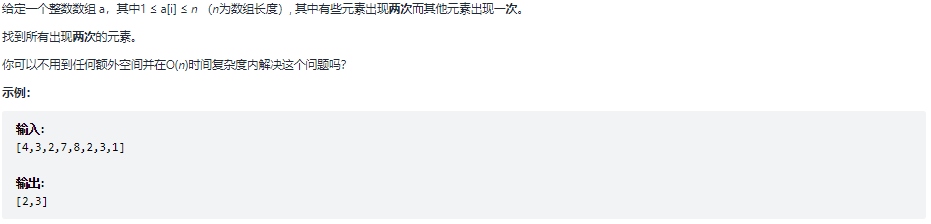
442.数组中重复的数据
题目:
1 | //排序后前后数值对比,重复的加入到结果中 |
1 | //哈希标记 |
41.缺失的第一个正数
题目:
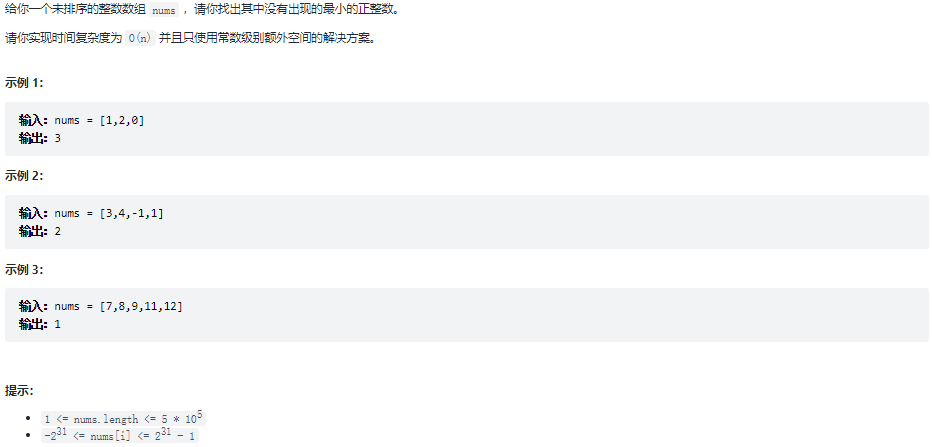
1 | /*哈希表记录(参考力扣官方解析,来源:力扣(LeetCode)) |
274.H指数
题目:
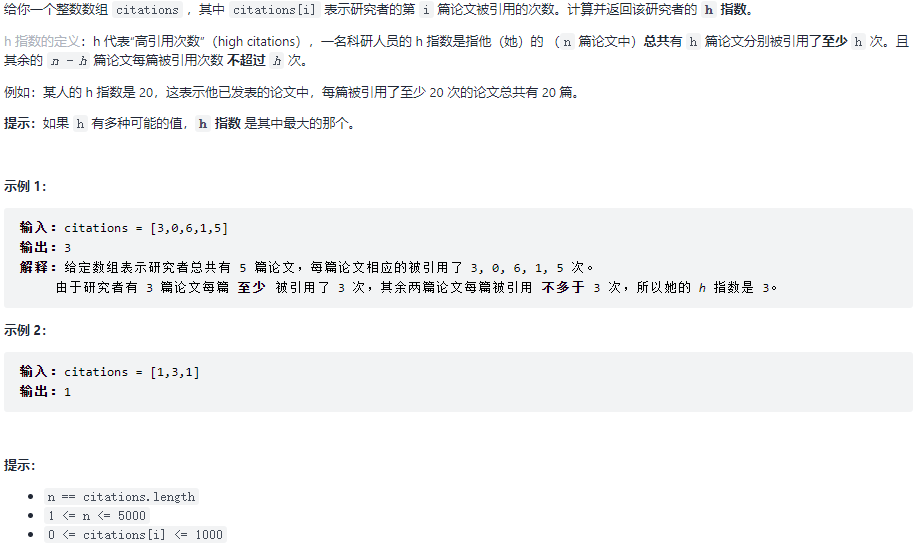
1 | /*排序法 |
1 | /*数组计数 |
2.3、数组的改变、移动
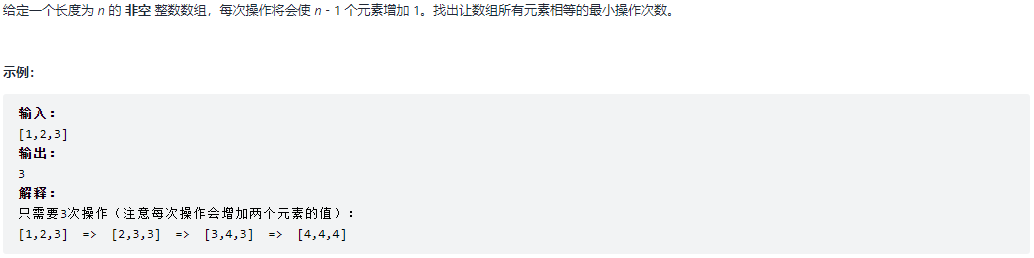
453.最小操作次数使数组元素相等
题目:
1 | /*排序法 |
283.移动零
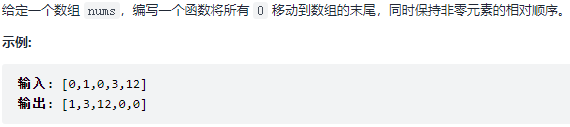
1 | class Solution { |
2.4、二维数组及滚动数组
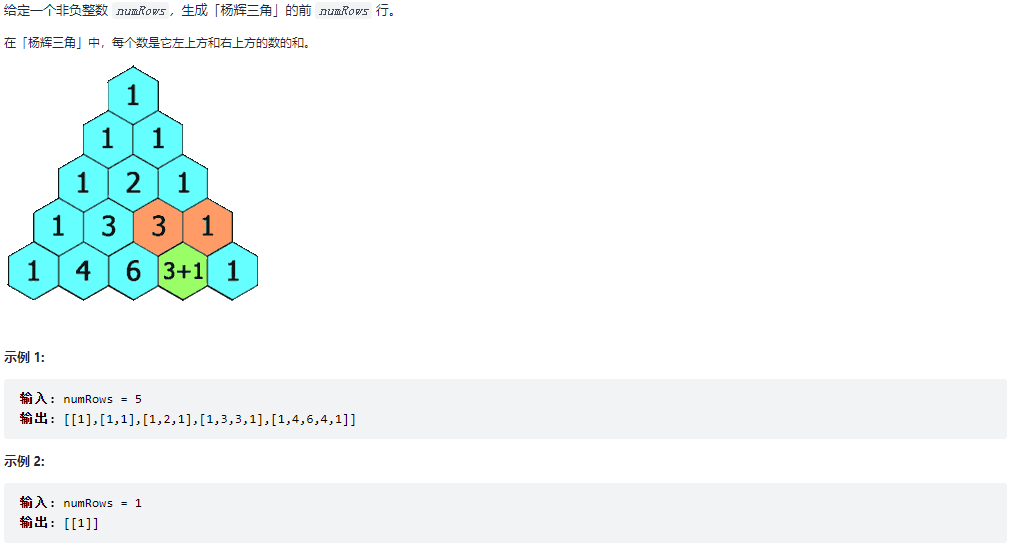
118.杨辉三角
1 | class Solution { |
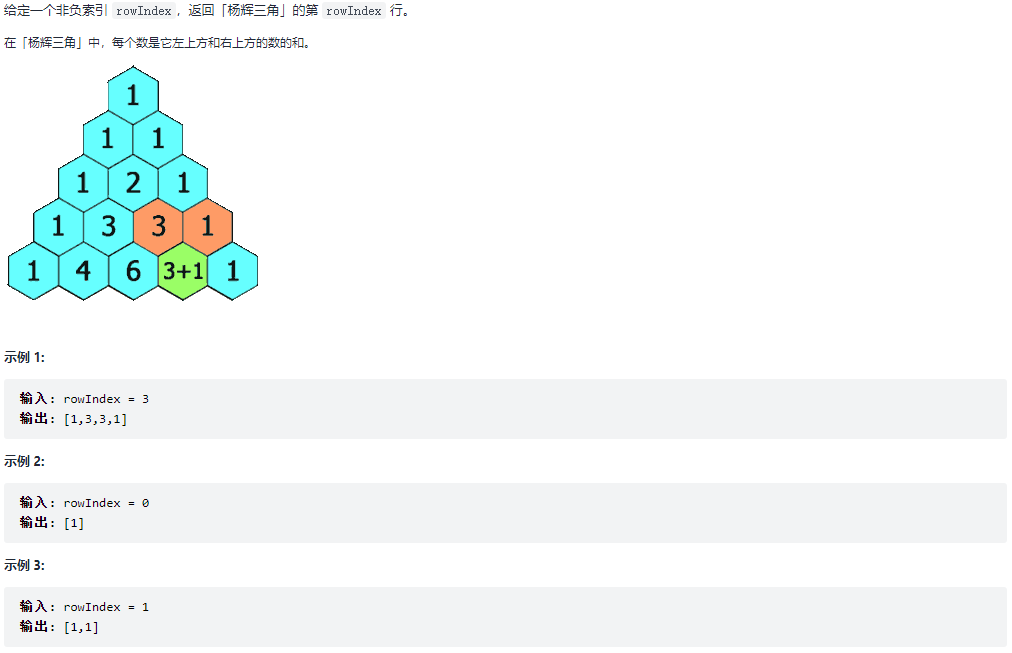
119.杨辉三角II
1 | class Solution { |
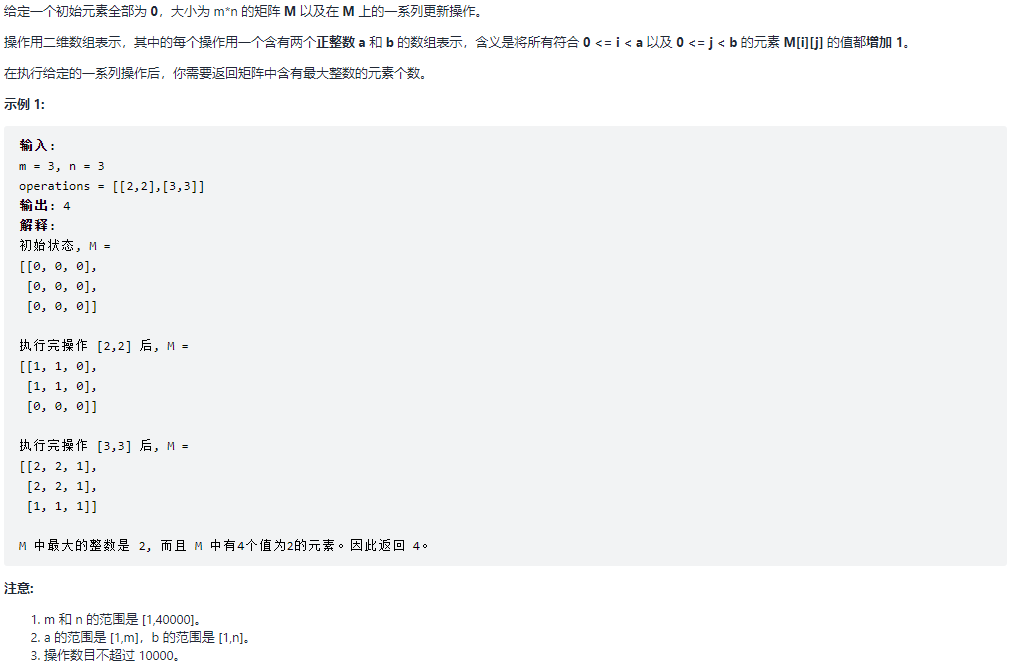
598.范围求和II
1 | /* |
2.5、数组的旋转
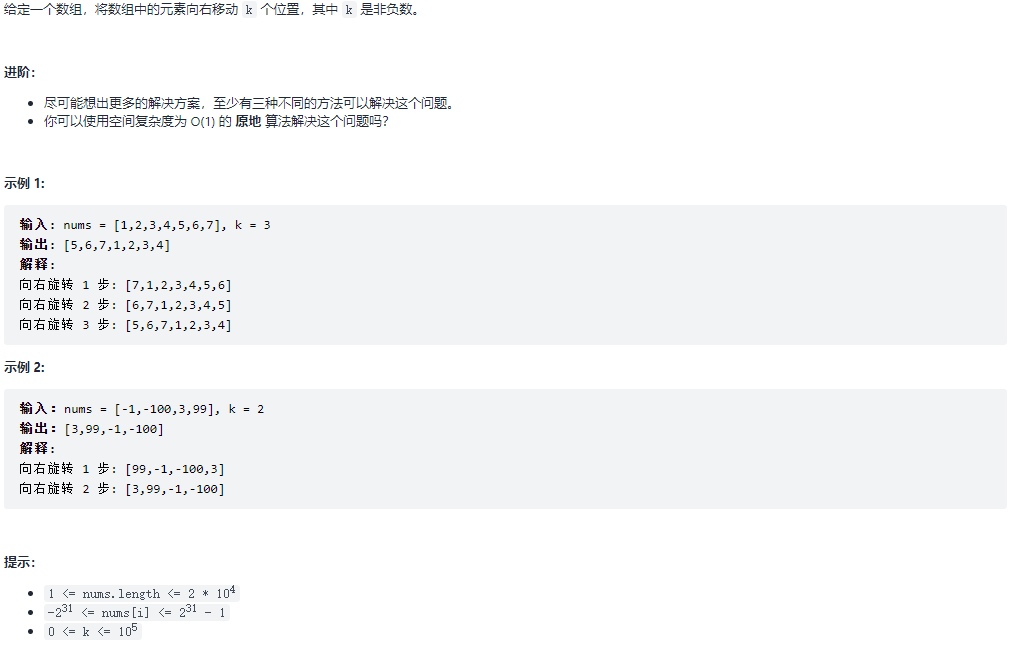
189.旋转数组
题目:
1 | // 直接暴力解法(超时),直接一个一个的移动 |
1 | // 数组反转(参考力扣官方解析) |
| 操作 | 结果 |
|---|---|
| 原始数组 | 1 2 3 4 5 6 7 |
| 翻转所有元素 | 7 6 5 4 3 2 1 |
| 翻转[0, k mod n-1]区间的元素 | 5 6 7 4 3 2 1 |
| 翻转[k mod n, n-1]区间的元素 | 5 6 7 1 2 3 4 |
396.旋转函数
题目:

1 | // 在上一题的基础上修改(超时),每一翻转一个数,计算总和比大小。 |
方法二:错位相减法
(作者:yixingzhang 链接:https://leetcode-cn.com/problems/rotate-function/solution/qian-lu-qi-qu-wang-wo-men-ke-yi-hu-xiang-iqax/](https://leetcode-cn.com/u/yixingzhang/))
$$
F(k) = 0 * A[0] + 1 * A[1] + … + (n-1) * A[n-1] \
F(k+1) = 0 * A[n-1] + 1 * A[0] + 2 * A[1] + … + (n-1) * A[n-2] \
F(k+1) - F(k) = -(n-1) * A[n-1] + 1 * A[0] + 1 * A[1] + … + 1 * A[n-2] \
F(k+1) = F(k) - n * A[n-1] + 所有数的和 \
F(k+i) = F(k+i-1) - n * A[n-i] + 所有数的和
$$
1 | // 用到了数学的错位相减,可能不一定能想到 |
2.6、特定顺序遍历二维数组
54.螺旋矩阵
题目:

1 | /* |

59.螺旋矩阵II
题目:

1 | /* |
498.对角线遍历
题目:
1 | /* |
2.7、二维数组变换
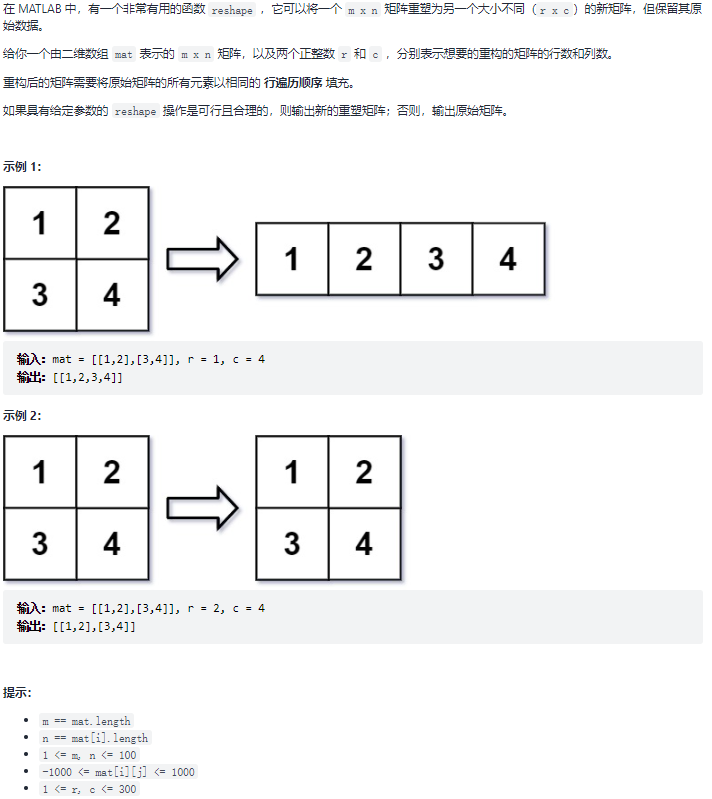
566.重塑矩阵
题目:
1 | /* |
1 | /* |
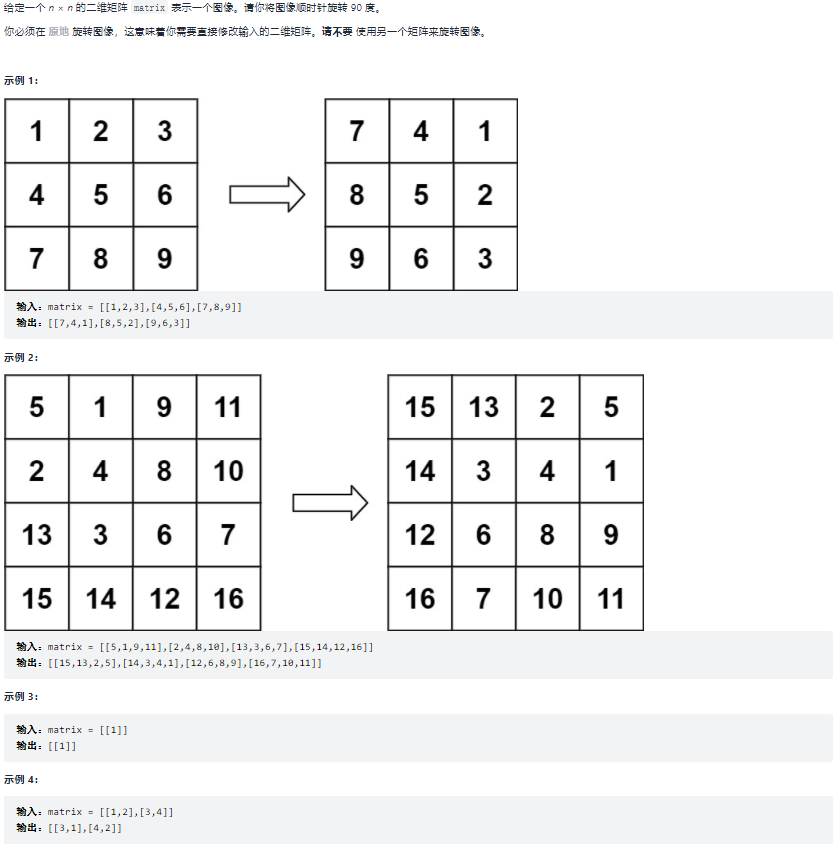
48.旋转图像
题目:
1 | /* |
73.矩阵置零
题目:

1 | /* |
2.8、前缀和数组
303.区域和检索-数据不可变
题目:

1 | /* |
304.二维区域和检索 - 矩阵不可变
题目:
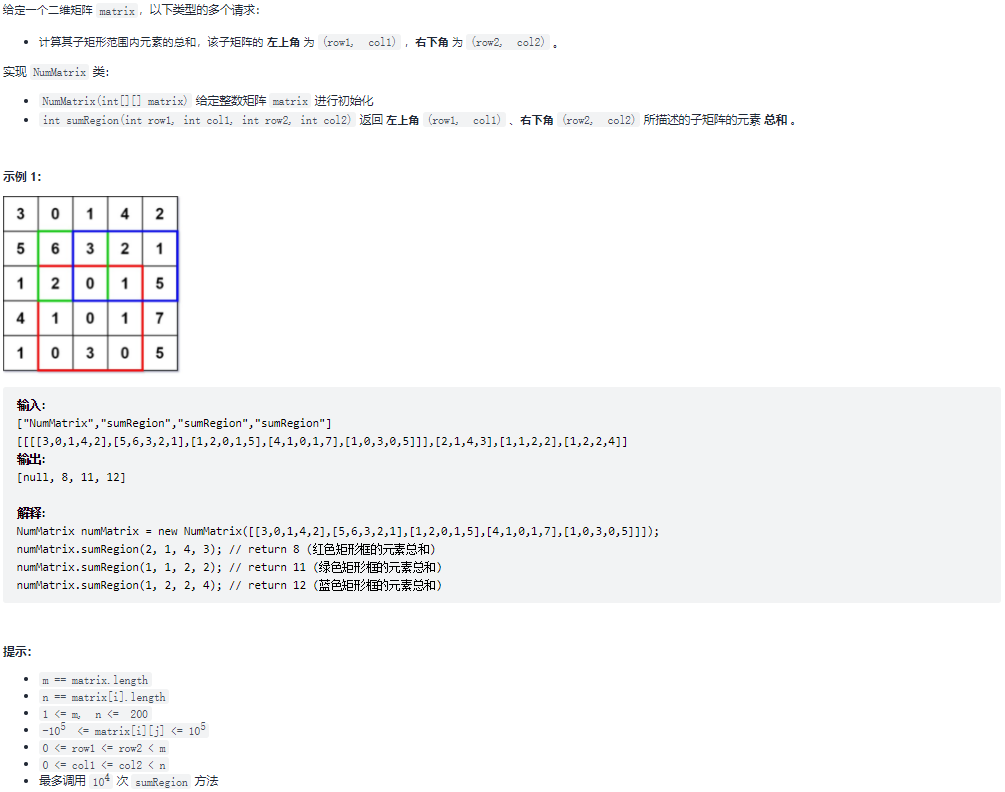
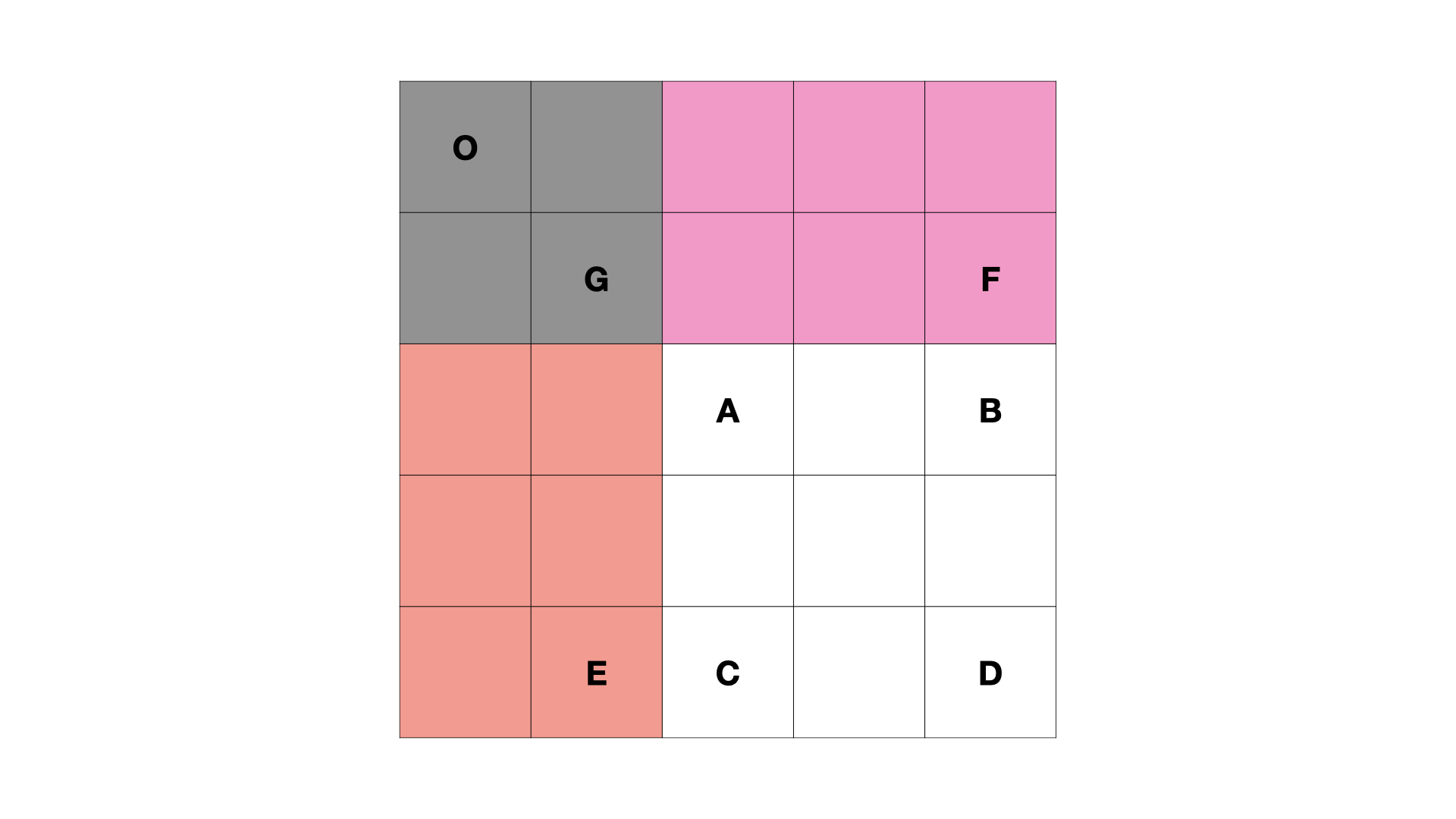
1 | /* |
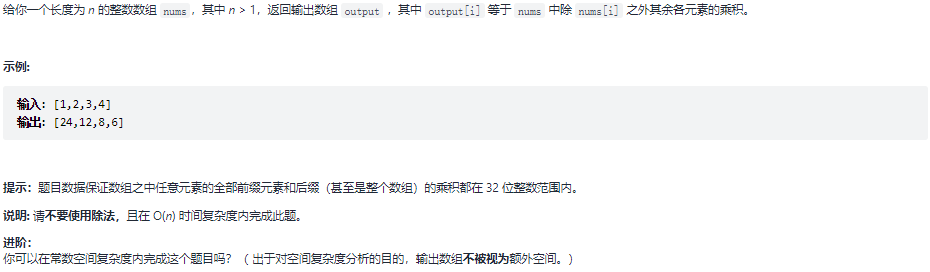
238.除自身意外数组的乘积
题目:
1 | /* |